本文通过对顺计时与倒计时两种不同计时方式的考察,提出一种新的看法,认为在顺计时下(时间坐标为t),时间间隔自然用时间坐标改变量Δt 来表征;而在倒计时下(时间坐标为),则必须用时间坐标改变量的相反数—Δ来表征。
把两种做法统一起来,则有:时间间隔应该用时间坐标改变量的绝对值来表征。
一、什么叫时间间隔?
通常人们所说的时间,包含“时刻”与“时间间隔”两个内容。“时刻”是指某事件发生的瞬间,例如高铁列车在上午10点15分开出。“时间间隔”是指不同瞬时之间的一段时间,用来说明某一事件持续的久暂,例如一场足球踢了1个半小时。简单地说,时刻是表示什么时候,时间间隔是表示某段时间有多长。
不言而喻,时间间隔不能是负数,如—5秒,—30分钟;它是正定的,即只能取正数,如5秒,30分钟,6小时等等。如果有人说:他走20米路花了—5秒。别人会以为,他可能是果克星球的智慧生物。
二、什么是时间坐标改变量?
物理学中,人们采用参数t来表示时间坐标。时间坐标改变量就是:用较晚时刻的时间坐标值减去较早时刻的时间坐标值得到的量。时间坐标改变量用符号Δt 来表示,较晚时刻和较早时刻分别用t晚和t早来表示,于是有:
Δt = t晚—t 早 (1)
.
三、时间间隔与时间坐标改变量的绝对值
物理学中,时间间隔由时间坐标改变量Δt 来表征。
1、这一做法,在顺计时下没啥问题。
这个没啥问题,并不是说t只能取正值。时间坐标t有计时零点:t0=0 ;比计时零点较晚的时刻t自然取正值,而比计时零点较早的时刻t则取负值。
没啥问题是指,顺计时的时间坐标t是单调递增的,较晚时刻的时间坐标值t 晚,总是大于较早时刻的时间坐标值t早,即t晚>t早
,因而可以保证时间坐标改变量Δt为正值:
Δt = t晚—t 早> 0. (2)
2、这一做法,在倒计时下就行不通了。
在倒计时下,不妨采用参数来表示时间坐标。于是,时间坐标改变量Δ为:较晚时刻的坐标值晚减去较早时刻的值早
所得到的量,即
Δ = 晚— 早 (3)
.由于 是单调递减的,其较晚时刻的值总是小于较早时刻的值,即晚< 早,因而总有
Δ = 晚— 早<0. (4)
显然,只能取正值的时间间隔,就不能再用时间坐标改变量Δ来表征,而应改用时间坐标改变量的相反数 —Δ来表征:
—Δ = 早— 晚>0. (5)
3、把顺倒计时两种方式综合起来考虑,则有统一说法如下:时间间隔应该用时间坐标改变量的绝对值来表征。即在顺计时下,时间间隔为
|Δt|=Δt = > 0 ; (6)
在倒计时下,时间间隔为
|Δ |=—Δ >0. (7)
四、顺倒计时方式下的速度公式
作为我们新见解的一种应用,我们来分析一下质点的速度公式。考虑一种简单情形:就质点朝x轴正向的某一直线运动,两位观察者分别用顺计时和倒计时方式加以考察。
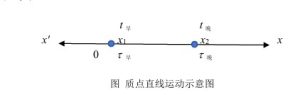
图 质点直线运动示意图
设质点从x1出发运动到x2。采用顺计时的观察者把质点出发时刻记为t早,把到达时刻记为t晚,则时间间隔为
|Δt|=Δt = t晚—t早> 0. (8)
在时间间隔Δt 内,质点的位移为
Δx=x2 — x1. (9)
于是,质点在这段时间内的平均速度为
v=A x/At. (10)
对同一质点运动,采用倒计时的观察者把质点出发时刻记为早,把到达时刻记为晚,则时间间隔为
|Δ|=—Δ=早—晚>0. (11)
在时间间隔—Δ内,质点的位移为Δx;质点在这段时间内的平均速度为
V倒= / A x/A (12)
由
—Δ=Δt, (13)
得到
v顺= v 倒 (14)
显然,这是正确的结果。
如果采用倒计时的观察者,习以为常地以为时间间隔仍用时间坐标改变量Δ来表征,则就会写下如下平均速度公式:
v倒=Ax /A=Ax /—At=— v 顺 (15)
这样,在他眼里分明是朝x轴正向运动的质点,上述速度公式却荒唐地表示:质点是朝x轴之负向——x'方向在运动!
无疑,式(15)是错误的。
式(15)的错误,提示我们要特别注意:时间反演物理学中的所谓“速度反向”,究竟是什么名堂。
2025年2月02日初稿
2025年5月21日修改



