导读：我们的《在弱相互作用领域之外，宇称守恒定律就不成立》[1]一文，对量子力学中的两个实际例证作了认真考察，进而对宇称守恒定律进行了明确的证伪。在该文结尾处，有如下尖锐的发问：所谓宇称守恒定律，究竟是否确实存在？人们在把它推导出来的时候，有没有出错？如果有，到底错在哪里？还有我们当真的承诺：在下一篇文章中，将给出自己的回答。

在本文中，我们依诺给出了答案。我们发现：至少有两种得到物理学界公认的宇称守恒定律之典型证明，是有明显谬误的，是站不住脚的。从而我们有理由认为：宇称守恒定律，恐怕不是什么局部不成立的问题，而是很可能压根儿就并不存在。

无疑，我们的上述发现，仍然必须依重对公式的运用。对我们的推理过程来说，由式(3)至式(17)的15个有点显得深奥的公式，是不可或缺的。好在我们的下一篇文章，就只有两个用来示意的简单式子了。我们在下一篇文章中，将用科普文章的标配笔触，讲述我们对物理学史上很有名的之谜的看法，评述68年前物理学家对之谜的艰辛破解，给出我们的独特破解之道。文章的标题已然觅得：无谜可言的之谜。

 

著名的宇称守恒定律是如何得到的？它是被物理学家用“严格的”推导过程证明出来的。我们在众多量子力学专著和教科书中，找到了两种典型的证明；并通过对上述两种证明的用心考察，发现它们均存在明显的谬误，都是站不住脚的。2009年9月，我们首次将上述发现公之于众[2]，并于2022年5月在自己的专著《物理学分立对称性新论》[3]中作了重申。

在推介我们的上述发现之前，仍有必要将量子力学教科书中的宇称守恒定律转述如下：

如果多个粒子组成的体系的哈密顿算符不是时间t的显函数，并在宇称变换下不变，即有

 

,                    (1)

 

则体系的定态波函数就具有确定的宇称：

 

,                    (2)

 

并且，这种由宇称量子数所表征的宇称不随时间而改变，即宇称守恒。其中，量子数+1表征波函数的偶宇称，量子数-1表征波函数的奇宇称。

现在，就让我们来看看宇称守恒定律的两种典型证明。

 

           一、第一种典型证明与我们的点评

 

在《时空对称性和守恒定律》[4]这部专著中，专门列有一节是谈宇称守恒定律的，并且详细给出了该定律的证明。这里，我们将书中的证明过程转述如下：

考虑到微观粒子的内禀宇称，具有确定角动量的微观粒子的状态可用下述波函数来描述：

 

.                       (3)

 

于是，我们有宇称变换后的波函数

 

,                        (4)

 

式中为总宇称算符，为粒子的空间宇称，它是粒子态的宇称和内禀宇称的乘积。

波函数满足薛定谔方程

 

.                         (5)

 

将上式两边乘以(-1)P，得到

 

,

 

即有

 

.                  (6)

 

算符与时间无关，所以和是可对易的，于是就有

 

,  引用式(5)即有

 

.                       (7)

 

式(7)表明和是可对易的

 

.                               (8)

 

而只要力学量的算符与哈密顿算符是可对易的，这个力学量就是一个守恒量。因此，我们又得到了一条守恒定律，即宇称守恒定律。

这条定律可作如下表述：在没有外来影响的条件下，量子体系内部不论其运动如何复杂，不论发生如何剧烈的变化，其宇称是不变的，原来奇者仍然为奇，原来偶者仍然为偶。

不难发现，上述证明过程的谬误是相当明显的。

我们知道，具有确定角动量的微观粒子态是角动量算符的本征态，它是有确定宇称的态，即当量子数l为偶数时，它为偶宇称态；当l为奇数时，它为奇宇称态。对于这样一个特定的定态波函数，当人们得到式(7)后，是不能进而推得式(8)的。只有对满足式(1)前提的任意定态波函数式(7)成立时，我们才能说和是可对易的，才能有式(8)的成立。

因此，文献[4]所得到的宇称守恒定律是虚妄的。

我们再来看宇称守恒定律的另一种典型证明，它载于《量子力学》[5] 这本教科书中。

 

二、第二种典型证明

 

设体系的哈密顿算符在宇称变换后保持不变：

 

.                  (9)

 

对于任意（定态）波函数，我们有

 

=.                                    (10)

 

所以

 

.                             (11)

 

这表示宇称是运动积分，即宇称算符对时间的全微商等于零：

 

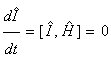,                            (12)

 

和必定有完全的共同本征函数系，因此体系的能量本征函数必定有确定的宇称，并且不随时间而改变。这就是量子力学中的宇称守恒定律。

 

三、我们对第二种典型证明的点评

 

考察这一证明过程，我们发现，它注意到了算符可对易的定义，没有像文献[4]那样采用特定的波函数，而是采用了任意波函数。然而，该证明过程存在两处明显的谬误，它们均发生在式 (10)之中。

第一处谬误为：当我们写下时，意味着必须先由哈密顿算符作用于得到一个新的函数，然后宇称算符再对新的函数施加作用。而写下，则意味着先由作用于得到一个新的函数后，再由对新的函数施加作用。当为任意波函数而两种不同顺序的作用结果相同时，我们就说算符和是可对易的。然而，文献[5]给出的证明，却在式(10)中居然由先对施加作用——这种做法肯定是不正确的。

试举一例说明如下。设有算符x和算符，它们按如下顺序作用于任意函数：先由x作用，再由作用。正确的运算是

 

.                           (13)

 

如果先由作用于x，就将得到错误的结果：

 

.                             (14)

 

显然，文献[5]给出的运算是错误的，因而它得到的结论必将是站不住脚的。

第二处谬误为：即便先对发生作用，也不可能得到下式

 

,                      (15)

 

而只能得到下式

 

 =.                       (16)

 

因此也就无法得到证明者很想看到的

 

                         (17)

 

之结果了。

由此可知，文献[5]与文献[4]一样，所得到的宇称守恒定律也是虚妄的。

 

我们真诚期待读者评述我们的上述纠错是否能够成立，并期待读者提供我们尚不了解的第三、第四种证明。现在，我们还不能下断言。不过，通过考察上述两种典型的证明，我们目前有理由认为：宇称守恒定律，恐怕不是什么局部不成立的问题，而是很可能压根儿就并不存在。

我们的下一篇文章，将讲述我们对物理学史上很有名的之谜的看法，评述68年前物理学家对之谜的艰辛破解，给出我们的独特破解之道。文章的标题已然觅得——无谜可言的之谜。

2025年11月30日 初稿于北京家中

2025年12月05日 定稿于北京家中

 

参考文献：

[1]江棋生. 在弱相互作用的领域之外，宇称守恒定律就不成立. 2025年11月29日发布于微信公众号“阿斗凿墙”、《光传媒》和《民主中国》网刊.

[2]江棋生. 质疑量子力学中的宇称守恒定律[OL]. 序号1512，自然科学—物理学，中国预印本服务系统，国家科技图书文献中心网，2010.09.08.

在网上搜索一下，就能见到这篇文章；或去我的《科学网》博客，也能找到这篇文章.

[3]江棋生. 物理学分立对称性新论[M]. 武汉：汉斯出版社，2022:136-140.

汉斯出版社关于此书的荐读网页：

https://mp.weixin.qq.com/s/2rlTYJejUuWzWJLNZV7_aQ

[4]卓崇培，刘文杰. 时空对称性和守恒定律[M]. 北京：高等教育出版社，1982：161-163.

[5]周世勋. 量子力学[M]. 上海：上海科学技术出版社，1961：137-138.