在本文中，我们就两个量子力学中的实际例证进行分析，简捷明快地对宇称守恒定律进行了证伪，说明其的确不能成立。我们举出的例证是：一维自由粒子的定态波函数，及一维自由粒子受方势垒散射的定态波函数。
在我们的证伪过程中，由式(3)至式(9)七个必要的公式，起到了中流砥柱的作用。而我们知道，有些朋友和网友一见到公式就会头晕。因而在此，我们愿诚挚地对他们说：我们是别无选择，只能对公式依重有加啊。而你们，则大可对文中的公式视而无睹，只需读读我们的中文表述，品品文章的逻辑架构；接着，再把文章转发给懂点物理学的朋友和后生就行。
1957年1月，吴健雄实验出了结果，宇称守恒定律遂在弱相互作用领域中被“证伪”——这是一桩即刻轰动世界物理学界的重大事件。不过自那之后，人们形成了一个坚定的共识：宇称不守恒仅仅发生在弱相互作用中，在电磁相互作用、引力相互作用和强相互作用中，宇称守恒定律完全无恙、照样成立。
现在，我们要对上述共识提出质疑：在弱相互作用领域之外，宇称守恒定律果真能够妥妥地成立吗？
为此，我们有必要首先将现有理论中的宇称守恒定律转述如下：
如果多个粒子组成的体系的哈密顿算符不是时间t的显函数，并在宇称变换下不变，即有
, (1)则体系的定态波函数就具有确定的宇称：
, (2)并且，这种由宇称量子数所表征的宇称不随时间而改变，即宇称守恒。其中，量子数+1表征波函数的偶宇称，量子数1表征波函数的奇宇称。
接着，我们就来考察量子世界里的两种情形：一种是一维自由粒子的运动；另一种是一维运动粒子受方势垒散射的问题。这两种情形都发生在弱相互作用领域之外。
我们先考察一维自由粒子的运动。
一维自由粒子的哈密顿算符为，
它不是时间的显函数，并显然满足。
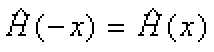. (3)因此，按照宇称守恒定律，一维自由粒子的定态波函数必定具有确定的宇称。
然而我们看到，它的两个定态波函数为
,
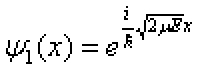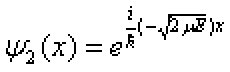, (4)
为沿轴的正向运动的自由粒子波函数，
为沿轴的负向运动的自由粒子波函数。显然
,
,
, (5)即
和均为x的非奇非偶函数，也就是说，自由粒子定态波函数并没有确定的宇称。这至少表明，对于一维自由粒子的运动，宇称守恒定律并不成立。
我们再来考察一维运动粒子受方势垒散射的问题。
所谓方势垒是指粒子受到势能为
(6)力场的作用，体系的哈密顿算符为
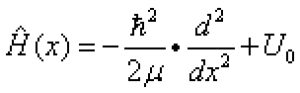, (7)它不是时间的显函数，并显然满足
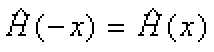. (8)而体系的定态波函数为
, 
; 
, 
; (9)
, 
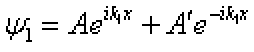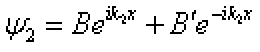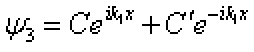.显然
，
，和
都不是x的奇函数或偶函数，即它们都没有确定的宇称。这就表明，对于一维运动粒子受方势垒散射的问题，宇称守恒定律也不成立。
至此，我们可以明确地断言：在弱相互作用领域之外，宇称守恒定律就这样被轻松地证伪了。也就是说，从这条定律被得到的那天起，它就不是量子世界中的普遍规律。上述断言，最早于2009年9月8日被我们公诸于世[2]。2022年5月，我们又在自己的物理学专著中对其加以重申[3]。
应当说，得出这样的断言，真的说不上有多大的困难；无需冥思苦想，更不用长篇大论，我们仅用了区区几百个字，就干成了。
令人感到十分纳闷的是，为什么自这个定律被提出近100年来，就一直没有人用自由粒子定态波函数去对它加以方便的证伪？甚至有人明确提到了“自由粒子定态波函数没有确定的宇称、该波函数不是宇称算符的本征态”[4]，也在只差半步之遥的地方停了下来，而没有得到一个势在必得的重要结论：至少对一维自由粒子的运动来说，宇称守恒定律并不成立。
直到1956年，人们因为所谓的
之谜才去质疑宇称守恒定律的普遍性，这实在是太晚了。而更大的遗憾是，人们仅仅质疑了一下它的普遍性，并得到了“在弱相互作用领域之外，宇称守恒定律还依然成立”的结论就完事了[5]。现在我们看到，在弱相互作用领域之外，宇称守恒定律早就并不成立。这就使我们必然要进一步发问：这个所谓的定律，究竟是否确实存在？人们在把它推导出来的时候，有没有出错？如果有，到底错在哪里？
在下一篇文章中，我们将回答上面的发问。
2025年11月28日 定稿于北京家中
参考文献：
[1]江棋生. 宇称守恒与左右对称毫无关涉. 2025年11月25日发布于微信公众号“阿斗凿墙”、《光传媒》和《民主中国》网刊.
[2]江棋生. 质疑量子力学中的宇称守恒定律[OL]. 序号1512，自然科学—物理学，中国预印本服务系统，国家科技图书文献中心网，2010.09.08.
在网上搜索一下，就能见到这篇文章；或去我的《科学网》博客，也能找到这篇文章.
[3]江棋生. 物理学分立对称性新论[M]. 武汉：汉斯出版社，2022:135.汉斯出版社关于此书的荐读网页：
https://mp.weixin.qq.com/s/2rlTYJejUuWzWJLNZV7_aQ
[4]卓崇培，刘文杰. 时空对称性和守恒定律[M]. 北京：高等教育出版社，1982：160-161.
[5]李政道. 弱相互作用和宇称不守恒(1957年12月11日在诺贝尔物理学奖颁奖典礼上的演讲)[A]. 诺贝尔获奖者演讲集：物理学1942-1964[R].
阿姆斯特丹：Elsevier 出版社，1964：406-418.
