即用|Δ |来表征。
现在,我们来考察顺倒计时方式之间的坐标变换关系。
设两位观察者对同一事件的进程,如运载火箭发射前最后10秒之进程,各自进行观察。一位采用顺计时;另一位采用倒计时,倒计时时段为10秒。10秒之后,火箭点火。对进程的每一时刻,两位观察者各自测得的时间坐标如下:
顺计时坐标t: 0, 1,2,3,4,5,6,7,8,9,10;
倒计时坐标:10, 9,8,7,6,5,4,3,2,1,0.
上述时间坐标t与的测量结果之间,存在什么关系呢?不难看出,时间坐标t与 之间有如下变换关系:
=-t+10. (1)
一般地,可设倒计时时段为D秒,则变换关系为:
=-t+D (2)
现在,我们对作一个平移变换
t'=-D (3)
则可立得:
t'=-t (4)
而式(4),正是人们早已熟知的时间坐标反射变换:
t-> t'=-t (5)
由此可知,时间坐标反射变换之真义,乃是顺计时与倒计时两种计时方式之变换,可简称为计时方式变换。t为顺计时坐标,—t为倒计时坐标;t和—t,表征相同的时间方向。
可叹的是,100多年来,人们却一直误把松枝标藤条,误以为:时间坐标t表征时间的正向流动,而时间坐标—t则表征时间的反向流动;因此时间坐标的反射变换(T变换),就是时间正反流向之间的变换,即所谓时间反演。例如,牛津大学彭罗斯教授在《皇帝新脑》[2]一书中说:
所有成功的物理方程都在时间上是对称的。它们在时间的任何方向上使用都显得一样。在物理学上,将来和过去似乎是平权的。牛顿方程、哈密顿方程、麦克斯韦方程和爱因斯坦引力场方程、狄拉克方程和薛定谔方程——如果我们颠倒时间方向(用—t来取代代表时间的坐标t),所有这些方程在实质上都不变。
在T变换的实质得以揭示之后,我们要引出一个重要的结论:由时间坐标反射变换即计时方式变换t→t'=—t所引发的物理量变换中,只有保持不变的偶变量,没有改变符号的奇变量。
在所谓“时间反演”下,以时间的一阶导数来表示的“速度”这一物理量,是典型的奇变量。那么我们就来看看,在倒计时t'下,质点的速度该如何求得。为简明起见,我们分析质点从x1运动到x2的变速直线运动,求出倒计时t'下,质点在这一运动过程中的平均速度,以及上述过程内某一时刻的质点瞬时速度。
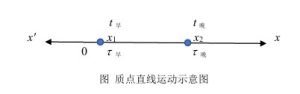
图质点直线运动示意图
参照文献[1],我们容易写出:在倒计时t'下,时间坐标改变量为
Δt'=t'晚—t'早<0, (6)
而时间间隔则为|Δt'|(对平均速度而言)和|dt'|(对瞬时速度而言):
|Δt'|=-Δt'=Δt; |dt'|=-dt'=dt (7)
于是,倒计时t'下的质点平均速度为:
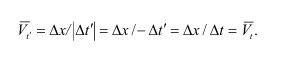 (8)
(8)质点瞬时速度为:
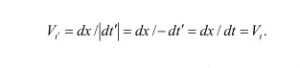 (9)
(9)式(8)和式(9)表明,在t→t'=—t的T变换下,速度这一物理量保持不变,并未反向。因此,速度是偶变量,不是奇变量。
那么,现有理论中的“速度反向”和“速度是奇变量”是如何得来的呢?那是因为,人们误认为在t'系下,时间间隔为Δt'(对平均速度而言)和dt'(对瞬时速度而言),他们有:
At'=-At; dt=-dt (10)
随之,质点平均速度就为:
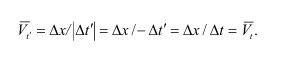 (11)
(11)质点瞬时速度则为:
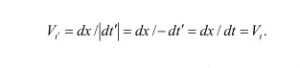 (12)
(12)于是,根据式(11)和(12),人们得出了T变换下“速度反向”和“速度是奇变量”的错误结论。
速度是时间的一阶导数;在t→t'=—t的T变换下速度保持不变这一事实,完全可以推广到一般情形:即任何以时间的一阶导数来表示的物理量,在时间坐标反射变换下均保持不变。因此,在时间坐标反射变换t→t'=—t下,只有偶变量,没有奇变量。
看来,已有100多年历史的时间反演物理学,将会被颠覆性地改写为计时方式变换物理学。
2025年3月30日初稿
2025年5月21日修改
参考文献:
[1]江棋生.时间间隔应该用时间坐标改变量的绝对值来表征.2025年5月21日
[2]彭罗斯R.皇帝新脑[M].长沙:湖南科学技术出版社,1995:351.



