上述教科书告诉我,这个矢量积一点儿也不神秘,它是一种矢量乘法运算——叉乘的结果:矢量A叉乘矢量B,得到一个新矢量C;矢量C,就叫作矢量A与矢量B的矢量积,并用记号 AxB来表示,即 C= A x B。(教科书中关于矢量积定义和矢量积基本性质的论述,我用附录一和附录二加以载明)。
不曾想,十七年后的1995年,当我开始对大自然展现的左右对称性感兴趣的时候,却颇为惊讶地知晓:在镜面反射操作下,矢量积这个根正苗红、地地道道的矢量,居然并不是真矢量,而是基因不纯、行为怪异的贋矢量。更具体一点说,就是在镜面反射下,上述矢量A和矢量B依然是矢量;但作为矢量乘法运算结果的矢量C,却生生成了另类——贋矢量。
那么,与矢量相比,贋矢量的“贋”体现在哪里呢?
现有空间反演理论告诉我们,矢量与贋矢量的重大区别在于:在镜面反射下,矢量平行于镜面的分量保持方向不变,垂直于镜面的分量要反向;而贋矢量的行为则正好相反,其平行于镜面的分量居然会反向,垂直于镜面的分量却又能保持方向不变。
在空间反演物理学领域,矢量积C是贋矢量这件事,早已是公认的共识。然而,经过多年的独立思考,我发现:矢量积C被戴上赝品帽子,其实是一桩学术冤案。
现在,就让我们来考察:矢量积C究竟是贋矢量,还是真矢量?
为了简明起见,我们设定矢量A和矢量B之间的夹角为直角,且矢量A垂直于镜面,矢量B平行于镜面。根据附录一,人们基于矢量A和矢量B的方向,将使用右手法则去确定矢量积C的方向:把右手的拇指顺着A的方向,食指顺着B的方向,则C顺着中指的方向。于是有:矢量积C的方向为垂直向上;矢量积C平行于镜面(图1)。
A A, =
现有理论告诉我们,在镜面反射下,矢量A和矢量B分别成了矢量A'和矢量B',且A'=-A , B'=B,即垂直于镜面的矢量A反了向,而平行于镜面的矢量B保持方向不变(图1)。那么,矢量积C之镜像C'的方向,究竟该如何去确定呢?
如果人们认为:既然我们作了规定,我们的世界是由右手法则来确定矢量积之方向的,那么镜像世界也应该根据同样的右手法则来确定矢量积的方向。于是,持有上述认知的人将基于矢量A'和矢量B'的方向,会在想象中把自己的右手伸进镜子里去确定C'的方向,即C'的方向由其右手中指方向所给出,这样就有C'=- C(图1)。也就是说,在镜面反射下,平行于镜面的矢量积C反了向。根据这一“实锤证据”,人们妥妥地认定:矢量积C显然不是真矢量,而是另一种玩意儿——贋矢量。
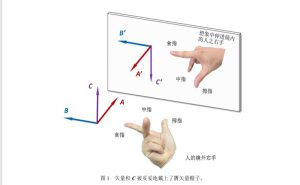
图1 矢量积C被妥妥地戴上了贋矢量帽子。
然而,矢量积C之镜像 C的方向,真是由人们把右手“伸进”镜子里去确定的吗?
我的见解是:矢量积C之镜像C'的方向,不能也不是由人们把右手“伸进”镜子里去确定的。我的上述见解,乃是基于简单的可观察事实:当人们在镜外用右手确定矢量积C之方向时,人们的镜像则共时地用其左手确定C之镜像C'的方向(图2)。这样我们就看到:在镜面反射下,矢量积C成了 C', C'的方向由人之镜像的左手中指方向所给出,于是有C'= C!这就是说,在镜面反射下,平行于镜面的矢量积C保持方向不变——这正是矢量性质的本真体现。
于是,我得到颠覆性结论如下:矢量积C乃是实实在在的真矢量;它的贋品帽子,完全是被冤枉戴上的。
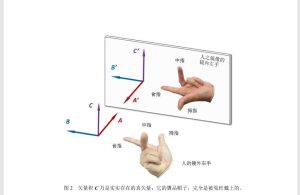
图2 矢量积C乃是实实在在的真矢量;它的贋品帽子,完全是被冤枉戴上的。
我的上述见解,在《镜中之核的旋转反向并未反转——与徐一鸿教授商榷》[2]中,有比较详细的叙述。极简说来,我的见解来自如下认知:对人的本尊来说,镜像世界虽近在咫尺,但却绝对的可望而不可即。无论多牛的高科技,无论多炫的人工智能,都无法助力人的本尊染指镜像世界。镜像世界中的行为主体,唯人的镜像莫属。
我们当然可以规定:我们的世界由右手法则来确定矢量积的方向,然而,我们岂能同时又规定:镜像世界也要由右手法则来确定矢量积的方向?这两条规定,肯定是相悖而不能并存的。只要想一想,如果我们规定我们世界的理发师只能用右手去理发,我们还能同时规定:镜像世界中的理发师也只能用其右手去理发吗?事实上,只要规定并严格实施“我们世界的理发师只能用右手去理发”,你就再也看不到镜像世界的理发师中,还有用其右手去理发的。
故此,矢量积C之镜像C'的方向,只能由人之镜像用其左手去确定,而决不是人在想象中把自己的右手“伸进”镜子里去标定的。
在本文中,我还将通过另一种方式,为矢量积C摘掉其被冤枉戴上的贋品帽子。
现有空间反演理论认定,在空间反演下,有关物理量的变换法则是:矢量(如A和B)要改变符号;而贋矢量(如矢量积C= AxB)则具金刚不败之身,保持不变。2025年1月7日,徐一鸿教授在发给我的电子邮件中重申了上述认定:“Then angular momentum, vector r cross vector p, clearly does not flip sign underspace inversion unlike a true vector.(作为矢量 r 和矢量 p 的矢量积的角动量,显然不会像真矢量那样,在空间反演下改变符号)”
那么,上述认定到底对不对呢?让我们剖析如下:
由附录一我们知道,三个有序矢量组A、B、C 组成右手系,即有C= AxB。
我们认为,如果上述有序矢量组经空间反演后所形成的有序矢量组 A'、 B'、 C',依然组成右手系,即有C' =A'x B' ,则A和B仍为矢量,而C则为贋矢量。因为这时有
C'= A'xB'
= (-A x-B)
= A xB
= C.
(1)
C保持不变,因而C是贋矢量。
然而,如果三个有序矢量组 A'、 B'、 C' 组成了左手系,即有C' =A'x B',则A、B、C均为矢量。因为这时有
C' =B'x A'
= (-B)x(-A)
=BxA
=-( AxB)
=-C .
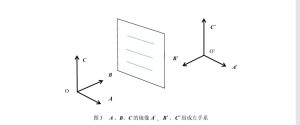
图3 A、B、C的镜像 A'、 B'、C' 组成左手系
(2)
那么,三个有序矢量组 A'、B'、 C' 到底组成了什么系呢? 我们认为,解决此事唯一可靠的办法是:对镜像进行老实观察,并作出如实描述(图3)。
不看不清楚,一看就明了:三个有序矢量组 A'、 B'、 C' 组成了左手系!这一事实,也可等价地表述为:三个有序矢量组B'、 A'、 C' 组成了右手系。
因此,我们的结论是:A、B、C均为矢量;现有理论中关于“两个矢量的矢量积是贋矢量”的认定,是错误的;所谓贋矢量,是完全不该出现的虚妄概念。
其实,从图3中我们可以得到更为简明直白、的观察事实:矢量积C的镜像C' 的方向,与C的方向完全一样,都是垂直向上。由此即可断言:矢量积C是真矢量,而决不是赝矢量。
既然贋矢量是虚妄的,那么,现有理论又是凭什么把矢量积C认定为贋矢量的呢?实话实说,这是一个扰我多年、令我脑疼的问题。不过,我总算幸运地找到了答案。一个原委就是:人们在想象中把自己的右手伸进镜子里去确定 C'的方向。另一个原委,则是来自下面似乎一目了然、充满底气的推导:因为A、B为矢量,所以在空间反演下有
A'=- A , B'=-B. (3)
而
C =AxB. (4)
所以,空间反演下必有
C' =A'xB'
=(-A)x(-B)
= AxB
= C. (5)
根据式(5),就能板上钉钉地认定:矢量积C为贋矢量。至于往镜子里瞧瞧能见到什么这类琐事,还有必要去分心、去思虑吗?!
第一个人这么做了,后面的人也这么做。谁也没去再想一想:C '=A'x B'到底对不对?它的依据又何在?
第一个人无心出了错,误以为 C '=A'x B'是对的;后面的人,则再也未曾加以审察,把其作为毋庸置疑的定论接受至今。
现在,我们先是点明:C '=A'x B'几何意义,乃是三个有序矢量组 A'、B'、C' 组成右手系。接着,我们判明:在空间反演下, A'、 B'、 C'并未组成右手系,而是组成了左手系,即有C' =B'x A'。其实,左右变换(空间反演)的固有魔力,就是将“右”统统变成“左”;把“左”统统变成“右”。因此,A、B、C组成的右手系被变成 A'、 B'、 C'组成的左手系,乃是题中应有之义。最后,我们
的结论是:在空间反演下,有且只能有
C' =B'x A'
=(- B)x(- A)
=BxA
=-(AxB)
=-C . (6)
亦即矢量积 C= AxB,乃是如假包换的真矢量。
不过,应当公正地说,矢量积C虽被戴上了贋品帽子,但却并没受冷遇,没被打入冷宫。相反,作为贋矢量的矢量积C像被赋予了特殊使命似的,成了空间反演物理学的一块重要基石。别的不说,由贋矢量派生出来的贋标量,就是一块不可多得的香饽饽:贋标量既是李政道、杨振宁获诺奖论文的核心概念和立论依据,又是吴健雄小组贝塔衰变实验的关键测量项。
尽管如此,我心目中好端端的真品成了贋品,对我来说,很难轻易不当回事。作为一个喜欢较真的人,我相信:假的真不了,真的也假不了。一样东西,是真是假,理应分清,不应弄错。
2025 年3月23日 初稿
2025 年4月01日 修改
2025 年5月18日 定稿
参考文献:
[1]樊映川等. 高等数学讲义上册[M]. 北京:人民教育出版社,1964:127.
[2]江棋生. 镜中之核的旋转方向并未反转——与徐一鸿教授商榷.2025年1月28日首发于网刊《光传媒》.致谢:文中图1和图2,是由江枫先生所绘。
附录一
两矢量的矢量积之定义
由两矢量A和B作出一个新矢量C,使矢量C满足下列三个条件:
(1) 矢量C的模C 等于 sin( , )A B AB 。这就是说,矢量C的模在数值上等于以两矢量A和B为两边的平行四边形的面积;
(2) 矢量C同时垂直于矢量A和B,因此,矢量C垂直于矢量A和B所决定的平面;
(3) 矢量C的正向按照“右手法则”来确定。这就是说,如果将三个矢量A、B和C附着于共同的起点,把右手的拇指顺着A的方向,食指顺着B的方向,则C顺着中指的方向(图7.17)。这样顺序的三个有序矢量组A、B、C在以后称为组成右手系。
这样,上述矢量C,就叫作矢量A与矢量B的矢量积,并用记号 AxB来表示,即C= AxB.
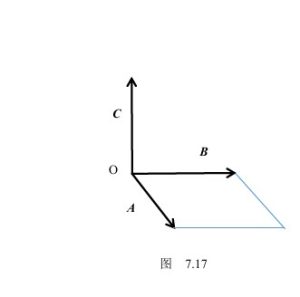
图 7.17
附录二
矢量积的基本性质

(1)当且仅当两矢量中之一为零矢量或两矢量平行时,其矢量积为零。
(2)矢量积对于因子的对调要改变符号,就是Bx A=-(Ax B ).
(3)矢量的矢量积与数量相乘有结合律的性质,即A B A B , (见图 )=A B A B .
(4)矢量的矢量积具有分配律的性质,即(A+B)x C =(Ax C)+( B xC) .
(附录一和附录二载参考文献[1]第127-129页)



